Unless you’re a math genius, you’re probably quite intimidated by calculus. The good news is, calculus isn’t as complicated as it seems, as long as you have a strong background in algebra, trigonometry, and geometry.
Whether you’re preparing for an upcoming semester of calculus class, or you’re looking for some extra help understanding what you’ve been learning, our basic guide to differential calculus can help. Once you’ve mastered the basics, you’re ready to take on more challenges.
What is Differential Calculus?

Calculus is a branch of math that’s focused on the study of continuous change. Differential calculus looks at the instantaneous rate of change.
So, what does that mean? We’ll use the speed of a car as an example. Your odometer gives you an estimate of how fast you’re driving, based on the distance you’ve travelled over the past few seconds. It works fairly quickly, but it’s not instant. If you wanted to know precisely how fast you were going at any given second, you’d need to use calculus to figure it out.
Before we can explain how to do that, we need to define some of the terms you’ll use in calculus so you can follow along with our basic guide to differential calculus.
History of Differentiation
Differentiation dates all the way back to the Greek era, such as Euclid, Archimedes, and Apollonius of Perga.
The modern-day calculus development is generally credited to Isaac Newton and Gottfried Wilhelm Leibniz who provided different approaches to differentiation and derivatives.
The main insight that earned them the accreditation of calculus is due to the fundamental theorem of calculus relating differentiation and integration.
Many other mathematicians have contributed to the differentiation theory since the 17th century.
In the 19th century, calculus became more rigorous by those such as Bernhard Riemann, Augustin Louis Cauchy, and Karl Weierstrass. Differentiation was then generalized to Euclidean space and the complex plane.
Functions

You’ve probably already covered functions in advanced algebra or trigonometry, so we’ll just do a quick review. A function is typically notated like this: f(x) = y, though there’s usually much more to it than that.
For an equation to be a function, any number you plug in as the (x) variable has to cause the equation to equal precisely one value of y.
An independent variable is a value of (x) in a function. It’s a number that you’re plugging into the function to change the output.
Dependent Variables
A dependent variable is whatever value is yielded by the function, represented in our example as y. The value of y will change depending on the value of (x), the independent variable. The value of the independent variable always determines the value of a dependent variable.
Domain
The domain of an equation or function is a set of all the possible values of the independent variable (x) that will produce a valid dependent variable (y). While the domain can be essentially infinite, for our purposes, we will create a relatively small domain.
For our little function, we’ll say that x can be [1, 2, 3…9]
The ellipsis (…) indicates that all numbers in between 3 and 9 are included in the domain. It’s just a more natural way of writing it, so you don’t have to list every number in the set.
Limit
The limit is the value that y approaches as x approaches a given value. If that doesn’t make sense, think of it this way:
In our domain, 9 is the highest value x can be. So, the limit of our function is the value of y as x gets closer to 9.
Typically, we use this with much larger domains, where the highest possible value of x isn’t known or doesn’t exist because it’s infinite. The limit allows you to define the pattern of values for y that you can extrapolate for any possible value of x.
Interval

Interval is a math term that isn’t limited to just calculus. It’s a set of numbers in between two given real numbers. Since those numbers can be broken down infinitesimally small, using an interval notation gives you a way to include all of those numbers without having to write them all out.
There are two main types of intervals: closed and open.
Closed Interval
A closed interval is expressed as [a, b] which is a set of all numbers between a and b, including a and b themselves. Using the variable x to represent the set itself, you can write this as a ≤ x ≤ b.
Open Interval
An open interval is expressed using parenthesis instead of brackets, (a, b). That is a set of all numbers between a and b, NOT including a and b themselves. You can think of it as a < x < b.
A half-open interval includes just one of its endpoints, meaning a ≤ x < b, or vice versa. It’s expressed as [a, b), or (a, b].
Derivatives
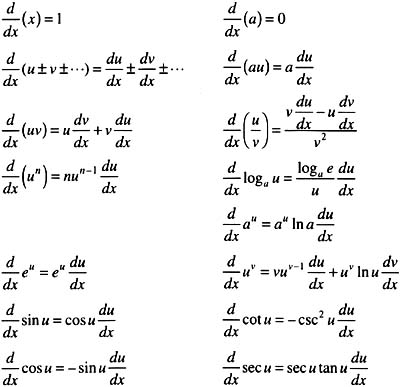
Derivatives are a special type of function that calculates the rate of change of something. Expressed in a graph, derivatives are the calculation of the slope of a curved line.
Derivatives are a fundamental concept of differential calculus, so you need to have a complete understanding of what they are and how they work if you’re going to survive the class.
Simply put, a derivative explains how a pattern will change, allowing you to plot the past/present/future of the pattern on a graph, and find the minimums and maximums.
There are several ways to represent the idea of derivatives:
- Derivatives measure the pitch of the line that represents a function on a graph, at one particular point on that line. That means derivatives are the slope.
- If the independent variable (the “input” variable in a function) is “time,” then the derivative is the rate of change, as the velocity.
- If we look at a short section of the line of the function so that the line is nearly straight, the derivative of that section is the slope of the line.
- The slope of a line connecting two points on a function graph approaches the derivative when the interval between the points is zero.
- As we mentioned before, derivatives are functions, and they’re always changing. When you find the derivative of a function everywhere, you get another function, which you can then solve for the derivative of, leading to another function, which you can get the derivative of, and so on. Each derivative tells you the rate of change of the previous function.
In a mathematical expression, the definition of derivative is:
In this function, h is a point on the line that’s very close to zero, and the limit is all of the tiny numbers between h and zero.
Derivatives and Polynomials
Finding the derivative of a polynomial would be very tedious using limits and the slope formula. However, there is another way to calculate the derivative of polynomials. We’ll work through an example, step by step.
First, you’ll need to multiply the exponent (2, as in x2) by the coefficient (2, as in 2x). Then we reduce the exponent by 1.
We ended up with – 5(x0) in the second term of the function by assuming the exponent in -5x could be written as -5x1, so we multiply it by the coefficient in front of the x, which is -5. Now we reduce the exponent by 1, which leaves us with 1*(-5)x0.
Anything to the power of zero is one, so ultimately we get 1*(-5)*1, which equals -5.
The third and final term of this function, +3, doesn’t have an x, which means it’s a constant. Following the same procedure as before, we start with 3x1. Multiplying the exponent by the coefficient, then reducing the exponent by 1, leaves us with 3x0. Once the zero comes down, we end up with 0 as our third term.
Our simplified derivative at the end of this process is:
The original function we started with was quadratic, but the derivative we ended up with is linear. The derivative will always be one degree less than the original function.
Other Rules and Theorems

There are a few other theorems you’ll need to learn in differential calculus, and memorizing them ahead of time will give you an excellent foundation for your calculus class.
Rolle’s Theorem
If a function is continuous on a closed interval and differentiable on the open interval (a, b), and f(a)=f(b) (the y’s on the endpoints are the same), then there is at least one number c in (a, b), where f′(c)=0.
Mean Value Theorem
If a function is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there is at least one number c in (a, b), where:
Intermediate Value Theorem
If a function f is continuous on a closed interval [a,b], where f(a)≠f(b), and m is any number between f(a) and f(b), there must be at least one number c in [a,b] such that f(c)=m.
 Photo credit to YouTube
Photo credit to YouTubeFinal Thoughts
We hope our basic guide to differential calculus has provided you with a solid foundation to build from in your class. Calculus can be a gratifying subject to learn because it has so many applications in the real world. And if you have any interest in physics or other sciences, calculus will go with it hand in hand!
Now that you armed yourself with all of this information, you should have no problem jumping into calculus head-first.