Entropy is the concept of chaos and disorder. It affects everything, including information. Learn how entropy works in calculus.
What Is The Entropy Information Theory In Calculus?
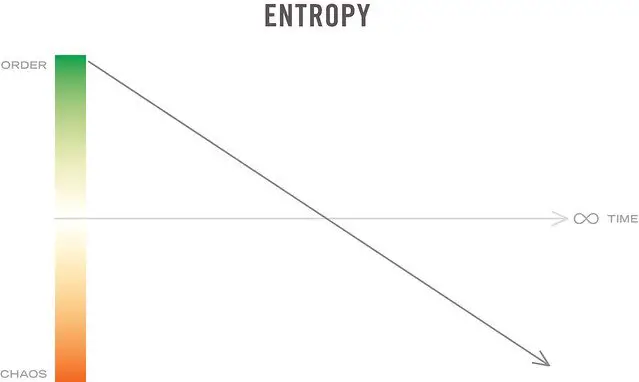
You’ve likely heard of the concept of entropy, or at least the word. Entropy has different specific definitions depending on the context in which you’re talking about it, but the common thread among the definitions is that of uncertainty and disorder. Entropy in any given system tends to increase over time when not provided with external energy or change.
Entropy, simply put, is the measure of disorder in a system. If you look at an ice cube floating in a mug of hot tea, you can think of it as an ordered system. The tea and the ice cube are separate. Over time, however, the heat from the tea transfers into the ice, causing it to melt and mix with the tea and leaving a homogenous mixture. There is no way to restore it to its previous state.
Everything in existence is subject to entropy per the second law of thermodynamics. There are several other definitions of the word, but what we’re here to talk about is the entropy information theory in calculus.
What Is Information Entropy?
What Does A Stand For?
Information is data about a system, an object, or anything else in existence. Information is what differentiates one thing from another at the quantum level. The entropy of information has more to do with probability than with thermodynamics: simply put, the greater the number of possible outcomes of a system, the less able you are to learn new information.
Following from this, it also means that a low-data system has a high amount of entropy. For example, a six-sided die when cast has an equal chance (unless you’re using weighted dice) of landing on any one of the six sides; the exact percentage of probability for any side landing face-up is 16.67 percent.
A 12-sided die would have a probability of 8.33 percent for landing face-up on any of the twelve sides. Its information entropy is even higher than that of the six-sided die.
As another example, if you have a regular coin with two sides, flipping it yields a 50 percent probability of landing on either heads or tails. The coin, because there is a higher probability for either outcome, has a lower level of entropy than does the die.
What Factor Influences The Level Of Entropy In A System?
The specific entropy information theory in calculus we’re talking about refers to data systems that have random outcomes, or at least some element of randomness. The level of entropy present in a data set refers to the amount of information you can expect to learn at any given time.
As such, the only factor that truly influences the level of entropy in a data set is the number of possible outcomes or the specificness of the information. For example, if you have a group of numbers from 1 to 10, and your only criteria is that the number is even, you only get one bit of information. It is measured in bits just as data in computers is.
Equation For Entropy
The equation used for entropy information theory in calculus runs as such:
H = -∑ni=1 P(xi)logbP(xi)
H is the variable used for entropy. The summation (Greek letter sigma), is taken between 1 and the number of possible outcomes of a system. For a 6-sided die, n would equal 6. The next variable, P(xi), represents the probability of a given event happening. In this example, let’s say it represents the likelihood of the die landing face-up on 3. Other factors being equal, you get 1/6.
Then, you multiply this by the logarithm base b of P(x), where b is whichever base you’re using for your purposes. Most often, you’ll use 2, 10, or Euler’s number e. For reference, e is approximately equal to 2.71828.
This, of course, represents only a single discrete variable with no other factors influencing it. If you have another factor that can influence the outcome, the formula changes. Now, it ends up being the following:
H = -∑i,j P(xi, yj)logbP(xi, yj)/p(yj)
In this case, you have to look at both x and y as variables and take their functions as dependent on one another, depending on how the problem is set up. You can also simply treat the two variables as two separate and independent events that occur. For example, f you were to flip two coins, you could treat x and y as each coin coming up heads or tails.
Alternately, you could assume that you had one coin coming up heads, which would trigger another coin flip whereas landing on tails would not. Then, you’d take y as the variable representing the second coin. Again, it varies depending on what you’re doing.
You can determine how much information is received from an event with a reduction of the formula to
-∑pilogpi.
You might notice that the log has no indicated base. This is because by default the base is 10. In computer science, when charting out probabilities, you might see base 2 used a lot because of binary systems. Base e is used in many scientific disciplines. Base 10, meanwhile, is used in chemistry and other sciences that aren’t quite as heavy on math.
Base 10, after all, is the basis of the decimal system and the one most people are used to working with.
The above formula represents the average amount of information you can expect to gain from an event per iteration. It assumes all factors are equal and there are no influencing conditions on the outcome. In other words, it is completely random within the available set of data.
How Is Information Measured?
Entropy information theory in calculus has several possible measurements, depending on what base is being used for the logarithm. Here are a few of the most common measurements:
On occasion, you may have to convert one measurement to another.
Purpose Of Studying Information Theory
One question that inevitably arises when dealing with higher mathematics is why it should be studied. After all, many skills in advanced math lack real-world applications, at least to the uninitiated. However, it should be noted that information and probability theory have several applications in computer science, such as file compression and text prediction.
For example, by using the entropy theory of information, you can help to code predictive text. The English language, for instance, has many different rules about what letters can occur in a sequence. If you see the letter ‘q’, you know that in all likelihood it’s followed the letter ‘u’. If you have two vowels, they will likely not be followed by a third, and certainly not by a fourth.
This is just one example. Another possible use in computer science is data compression as in ZIP files or image files like JPEGs. Information theory has also encompassed various scientific disciplines from statistics to physics. Even the inner workings of black holes, such as the presence of Hawking radiation, rely on information theory.
Even the act of learning higher math and abstract concepts can be beneficial, even without the knowledge. The act of learning forces the brain to process information in new ways, creating stronger connections between neurons and delaying the onset of cognitive decline. The more you learn, the more exercise your brain gets.
Understanding Information Theory
To get the most out of and understand information theory, you need a solid grasp on a few other subjects. These are all unsurprisingly math-related. Calculus and statistics are the two main subjects you need to study before starting to work on information theory because you’ll need to know how to take integrals and derivatives from calculus.
Statistics, meanwhile, gives you a solid understanding of probability theory and the likelihood of events occurring. You’ll also be introduced to a few of the more esoteric variables like lambda, or some of the symbols like sigma for summation if you haven’t seen them before.
You’ll also need to have a solid grasp of algebra, such as knowing how to manipulate equations and variables. Although you should get plenty of practice doing this in the course of algebra, it’s a good idea to understand some other concepts such as how to take a logarithm. As you can see, logarithms play a vital part in several of the entropy equations.
Final Thoughts
Learning the entropy information theory in calculus is a good way to understand how probability works and how many of the data systems you encounter produce various amounts of information. If you have a background in thermodynamic studies, it can make it easier to understand the concept of entropy.
Entropy in information theory is slightly different than it is in other branches of science, but the basic idea is the same.