Tired of solving messy expressions when working on integrals in calculus? Learn to use the substitution method and help clean them up.
What Is The Substitution Method In Calculus?
If you’ve studied calculus for any length of time, you’ve encountered integration and likely looked for different ways to work out an integral. The substitution method for integrals is nothing more than another way to find it, but bear in mind that it only works when the integral is written in a relatively simplified form, namely the product of a function and its derivative.
Using u-substitution makes it easier to read and simplify composite functions, which can otherwise start to look messy and intimidating.
This method is also called u-substitution. The idea behind doing u-substitution is to rewrite the integral into a form that easily fits with the known rules of integrals. We’ll look at these rules, go over the basics of what integrals are to provide a refresher, then go into how to do the substitution method. You can only integrate by using the known rules.
What Is Integration?
Integration in calculus is the idea of taking a generalized area underneath the curve of a function. It is impossible to get an exact area, but you can approximate it with an integral, which is the combination of different measurements of the area under a given curve. On a Cartesian graph, you would have to use rectangular or trapezoidal sections, but that isn’t accurate.
Of course, taking a higher number of thinner slices of x gives you a more accurate measurement of the area under the curve. In this case, x is the horizontal distance between the dividing lines you use to measure. The integral is what happens when x approaches zero. You can’t use a zero value for x, because there is no change in x to measure.
All of this said, there are some rules to integration you need to be aware of. We’ll run down a brief list of the most common ones. The expression ‘dx’ indicates that the change in x between points is infinitely small without being zero.

Known Rules Of Integration
These rules let you calculate the integral of almost any function. There are other rules of integration, but for now we’ll focus on the simplest and most useful.

Uses Of The Integral
Taking the integral gives you the closest possible measurement of the area under a function’s graph. You can take definite or indefinite versions. Taking a definite integral provides bounds on the two values of x, while indefinite ones focus on the whole function from negative to positive infinity.
Most practical applications will focus on definite integrals, which have their two values denoted as subscript and superscript next to the integral sign like this: ∫ab f(x) dx. In other words, you calculate the problem using the value of b, then the value of a, and use the difference.

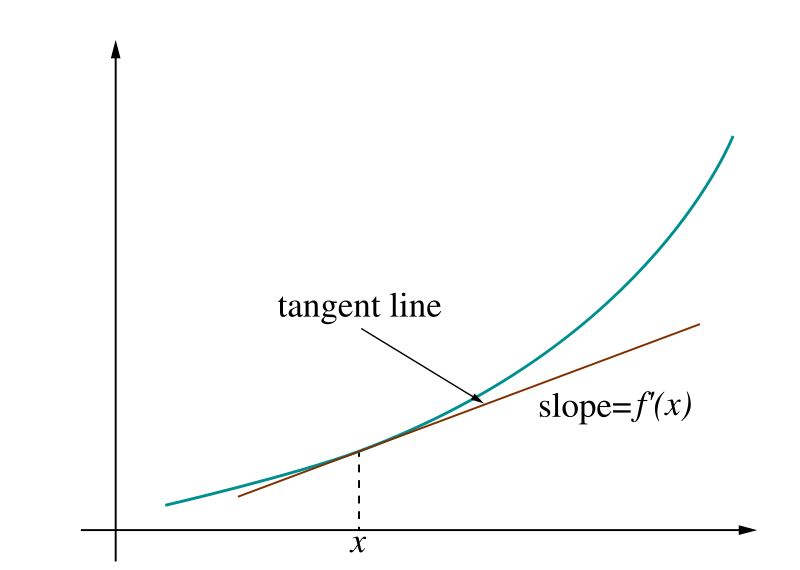
Derivatives
Since we know about integrals, we also need to look at derivatives because the two types of functions work together in calculus.
A derivative is nothing more than the rate of change of any function at a given point. Knowing these derivatives and their associated rules allows you to easily solve calculus problems when using the substitution method.
Here’s a list of some common derivative rules:
Substitution Rule
Now we’ll talk about the substitution rule. Using the u-substitution rule makes it easier to read and work with composite functions, i.e. (f(g(x)) by putting the variable u in place of the inner function, or g(x). You then multiply this by the derivative of u, also called du. Then, you place your original function in place of u and the derivatives, which gives you your answer.
Here’s how the method looks in an example problem.
We’ll start with ∫(x + 2)3 dx. The derivative of any line notated by m = ax + by + c is the variable a, which is the slope. Therefore, the integral could be rewritten as ∫(x + 2)3 * 1 dx. Now, you simply place u into the integral in place of the parenthetical expression like so: ∫(u)3 du.
Per the power rule, you can see that ∫u3 du = u4/4 + C. C is the constant of integration. In an indefinite integral, you can plug virtually any value into the function, and it will remain valid. Essentially, all you’re doing is shifting the graph of the function up or down, but not changing the actual graph. Also, the derivative of the constant is 0, so it has no real effect.
Getting back to the integral, from this step, you simply plug the original function back in where you substituted u. Completing this step yields (x + 2)4/4 + C, where again, C is the constant of integration if there was one.
Looking at another integral using the substitution method in calculus, let’s take ∫(2x + 3)4 dx. This one looks a little trickier at first, but it’s essentially the same concept. Substitute u into the parenthesis, making ∫(u)4 2 du.
Because you added the 2 into the expression, you need to do something to cancel it out, making the expression 1/2∫(u)4 2 du. Multiplying the expression by ½ effectively does this.
After this you’ll need to take the integral of the function. Do this using the power rule just like before. In turn, this yields you with ½ u5/5 + C. Putting the original function back into the equation, you get (2x + 3)5/10 as the integral.
These are just two of the simplest examples. Remember that you can only use the substitution method when the integral can be expressed in the form of ∫(f(g)x)) g d/dx, or ∫f(u) du.
Definite Integrals
We’ve talked about indefinite integrals up to this point, so let’s move on to definite ones. As we mentioned, a definite integral is solved in the same way as an indefinite one, except you’re putting in actual values for x and taking the difference between the two results.
Let’s go back to our original example of ∫(x + 2)3. This time, we’ll set bounds at 1 and 3. This puts the integral at ∫13(x + 2)3.
Now, we just have to rewrite our original integral: u4/4. Now, you’ll plug the original function back in as (x + 2), but this time, you’ll be putting in 3 for x: (3 + 2)4, or 54/4. 156.25 is the result. Then you’ll need to calculate the same for 1 as the value of x. (1 + 2)4 or 34/4. This result is 81.
Now, you just subtract 81 from 156.25, yielding 75.25 as the definite integral of the function.
Trigonometric Functions
You can also take the integrals of trigonometric functions in calculus. Sine, cosine, and tangent, are all possible to do. You can also get secant, cosecant, and cotangent, but aside from the secant, you don’t use the others much.
The tangent integral can also be expressed as ∫(sin x/cos x) dx, just as a regular tangent operation can be expressed as sin/cos. A good example is if you try to take the tangent of a 90-degree angle: the sine of 90 is 1, and the cosine is 0; the problem becomes immediately obvious. Likewise, the tangent of 0 is 0.
Drawbacks Of The Substitution Method
The substitution method in calculus is an excellent method in most cases, but it’s easy to get wrong for beginners. One of the biggest problems beginners have with this method is not substituting u for the whole expression. The variable u is meant to be the whole inner function f(x).
Another big problem is when beginners forget to add a constant to the outside of the integral, so it can be expressed in the proper form. For example, if you have 3x inside the integral, you’ll want to multiply the whole expression by ⅓ so the answer isn’t changed.
Final Thoughts
If you learn the substitution method early in your studies of calculus, you should have fewer problems when solving integrals and derivatives than you would otherwise. Some of the functions can look intimidating, but simplifying and expressing them in terms of u and the derivative of u cleans up the problem and makes it easier to solve.