A parallel plane is a flat, two-dimensional surface. If you have two planes that don’t intersect, they’re parallel. Use calculus formulas to determine the distance between two parallel planes. You can solve some problems by finding random points on the plane, and then use an equation to figure the distance.
What Are Parallel Planes In Calculus?
You probably deal with parallel parking now and then, so you may have a vague idea of the definition of parallelism and how it might be used with figures in calculus and geometry.
You’ll encounter parallel planes in your Calculus 3 classes, and focus on equations of planes and other problems.
Here’s a look at planes in calculus, and how parallelism relates to them. We’ll also look at parallel postulates, and how parallel lines and planes are used in geometry and calculus.
What Is A Parallel Plane?
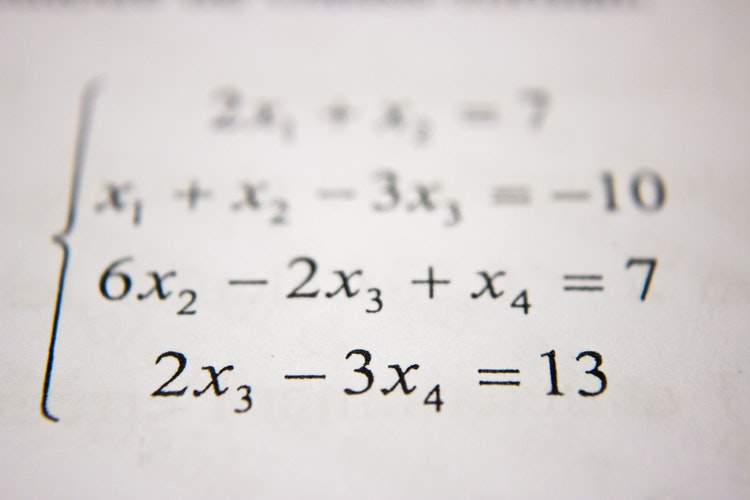
Image by Antoine Dautry
In calculus or geometry, a plane is a two-dimensional, flat surface. Two non-intersecting planes are parallel. You can find three parallel planes in cubes. The planes on opposite sides of the cube are parallel to each other.
Parallel lines are mentioned much more than planes that are parallel. They are the lines in a plane that don’t meet. A plane and a line, or two planes in a 3D Euclidean space are parallel if they don’t share a point.
Parallelism is used in Euclidean and affine geometry. Hyperbolic geometry may have lines with analogous features that fall under parallelism’s properties.
Skew lines are two lines in a 3D space that don’t meet in a common plane.
The Parallel Postulate
Image by Roman Mager
Euclid’s parallel postulate says that for every straight line and a point that’s not on it, there’s only one straight line passing through that point that doesn’t intersect the first line, regardless of how far the line or point are extended.
This mathematical postulate corresponds with Euclid’s Fifth Postulate. Euclid didn’t use this postulate until Proposition 29 of the Elements.
Many experts didn’t believe the Fifth Postulate was accurate but considered it a theorem taken from Euclid’s first four postulates. The term absolute geometry refers to geometry that is based on Euclid’s first four postulates.
Many parallel postulate proofs have been written and discussed by the mathematical community over the centuries.
The dissertation of G. S. Klügel in 1763 called Euclid’s parallel postulate a necessary tool to prove mathematical results. The postulate wasn’t intuitive, Klügel wrote, but it was helpful.
An axiom proposed by 17th Century mathematician John Wallis stated that a triangle could be changed to be larger or smaller with any distortion of its angles or proportions.
Lobachevsky and Janos Bolyai, in two separate 1823 studies, concluded that you could create non-Euclidean geometry that didn’t adhere to the parallel postulate.
The parallel postulate refers to modern day Euclidean geometry. Change the phrase so only one straight line passes or no line which passes exists, or two lines or more pass, you will be describing elliptic (no line passing) or hyperbolic geometry (two or more lines passing).
The following theorems and axioms are equal to the parallel postulate:
One of Hilbert’s parallel axioms is also equivalent to the parallel postulate.
Find The Distance Between Two Parallel Planes

Image by Helloquence
Our planes are II1 and II2. These planes are parallel if II1’s normal (n1 = a1 b1 c1) is the scalar multiple k of II2’s normal n_2 = (ka_2, kb_2, kc_2)
Example #1
Example #2
Example #3
Let’s look at the planes II2:4x+8y+12z+6=0 and II1:2x+4y+6z+1=0. Get the norms of these planes to arrive at n1=(2,4,6) and n2=(4,8,12) You’ll get 2n1=n2 and finally II1∥II2.
Find an arbitrary point on II1 or II2. After choosing your arbitrary point on one of the planes, use the equation for the other plane in the formula for the distance between a plane and point. You’ll now determine the distance between the two planes.
The planes II2x+3y+4z−3=0 and II2:−4x−6y−8z+8=0 are the basis of our second problem. Find a random point on the first plane, for example, 0,0, and four over 3, and then use formula D (distance) equals ax0 plus by0 plus cz0 plus d over the square root of a squared plus b squared plus c squared.
Now figure out the distance between the two planes using this formula.
D equals 4(0) plus negative 6(0) plus negative 8(3/4) plus 8 over the square root of negative 4 to the second power plus negative 6 to the second power plus negative 8 to the second power, followed by D equals negative 6 plus 8 over the square root of 16 plus 36 plus 64, then D equals 2 over the square root of 116.
Practicing With Parallel Planes

Image by Dawid Małecki
Remember to practice equations involving parallel planes several times, using problems other than those assigned by your teacher. There are plenty of practice questions in textbooks and online. You should also join a study group or contact a tutor if you need more practice with geometry or calculus.
Logical Learning In Calculus And Geometry
The logical or mathematical style of learning works for any subject, but it works best for algebra, geometry, and calculus. Logical learning enables you to recognize patterns easily and draw connections between content that may seem unrelated. You know how to group information do you arrive at a correct conclusion.
A person with a propensity for logical learning remembers the basics of geometry, algebra, and calculus without referring to a textbook. You can perform moderately difficult calculations in your head.

Image by Snapwire
You use a system to work through problems, and apply it to all types of equations and mathematical questions. Setting budgets and numerical goalposts helps you make progress when you solve complicated equations. A scientific thought process allows you to support your arguments with statistics and facts.
You should identify and point out flaws in other people’s’ logic, and work out strategies for all types of projects. You may play video games that involve detective work and strategizing simulated war plans. If you have a logical thinking style, you may like science, computer programming or law as well as mathematics.
You look for the logical way to solve a calculus or geometry problem. You strive to understand all the details behind why you perform certain steps in solving an equation. You aren’t satisfied with merely memorizing formulas. Explore the logical steps you use to apply to a problem, and keep them in mind when you tackle a new equation.
Don’t overanalyze when you work on a difficult problem. Work with the formula and prior knowledge of similar equations. If you don’t get the answer right at first, try again, but avoid developing “analysis paralysis” when figuring out what you did wrong.
The video may take a few seconds to load.
Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.