 2011-2012
2011-2012
Four functions are continuous and differentiable for all real numbers, and some of their values (and the values of their derivatives) are presented in the below table:
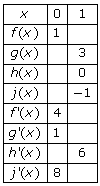
If you know that h(x) = f(x) · g(x) and j(x) = g(f(x)), fill in the correct numbers for each blank value in the table.
Solution:
Woo, Nelly, this is a bunch of work. Here’s the answer:

There are different ways to solve the problem, but here’s one step-by-step solution:
1. If h(1) = 0, then either f(1) or g(1) must equal 0, since the two are being multiplied. You know thatg(1) = 3, so therefore f(1) = 0.
2. Use the fact that h’(1) = 6 to figure out f’(1). Since h is a product, use the product rule to find its derivative.
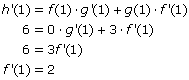
3. Since j(1) = –1, you can find an unexpected value, g(0), thanks to the fact that f(1) = 0.
![]()
4. Now you can figure out j’(1), since g’(0) = 1. Use the Chain Rule to calculate j’(1).
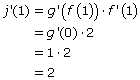
5. Now that you have all of the necessary pieces, you can calculate j(0).
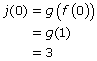
6. While you’re working on functions evaluated at 0, perhaps you’d enjoy calculating h(0).
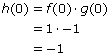
7. Because you know what the values of j’(0) and f’(0) are, you can calculate g’(1).
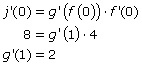
8. You only have h’(0) left, so return to the product rule.
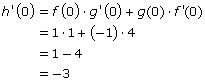
You don’t have to complete the steps in the order prescribed above, and there are other methods that work, but you should end up with the same final values in the chart.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






