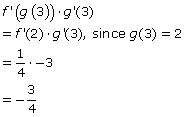2019-2020 Derivative Table
Two functions, f(x) and g(x), are continuous and differentiable for all real numbers. Some values of the functions and their derivatives are given in the following table.
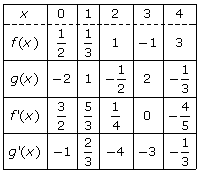
Based on that glorious table, calculate the following:
(a) 
(b) 
(c) 
(d)
Solution:
(a) Take the derivative of each function separately (the derivative of a sum is equal to sum of its derivatives) and plug in 4 to each to get your answer. Reference the chart for the values of f ‘(4) andg‘(4).
(b) This time you have to use the Product Rule, because f(x) and g(x) are multiplied. Once again, after you apply the derivative rule, just nab the needed function and derivative values from the chart.
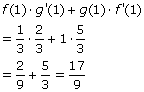
(c) This time it’s the Quotient Rule that has to be applied.
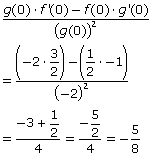
(d) How about a big, warm welcome for the Chain Rule! Remember, you apply the Chain Rule when one function is composed with (inside of) another. To differentiate, take the derivative of the outer functionf(x) while leaving g(x) alone inside f(x). Then multiply by the derivative of g(x).
