 2011-2012
2011-2012
During a taping for Circus of the Stars, beloved actress Betty White is shot out of a cannon. The firing goes completely awry and sends her on a collision course with a jet. As they converge, Betty and the jet plane at right angles to each other (see diagram below). Betty is 200 miles away from the point of impact and traveling at a constant rate of 600 mph. (Not even the laws of physics can slow Betty White!) The plane is 150 miles from impact and traveling at a constant rate of 450 mph.
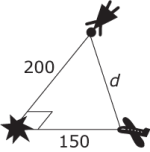
At what rate is the distance d between Betty and the jet decreasing?
Solution:
Consider the following diagram, which labels the legs of the right triangle as follows: b is the distance between Betty White and the point of impact and p is the distance between the plane and the point of impact.
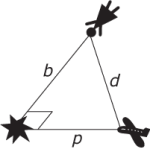
The Pythagorean Theorem describes the relationship between the lengths of the sides of the triangle.
b2 + p2 = d2
Substitute b = 200 and p = 150 into the formula to solve for d, the distance between the two airborn objects at this moment.
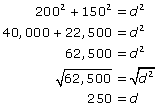
You are asked to find the rate at which d decreases. In other words, you are calculating dd/dt. Apply implicit differentiation, with resepct to t.
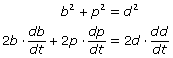
Divide each of the terms by 2 and solve for dd/dt.
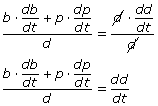
To calculate dd/dt, substitute all of the known information into the equation: b = 200, db/dt = –600, p = 150, dp/dt = –450, and d = 250. Note that db/dt and dp/dt are negative because the lengths of the legs of the right triangle are decreasing—the objects are on a collision course, so the distances between the objects and the point of impact are getting smaller.
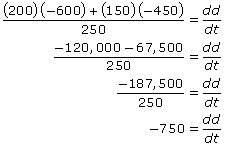
The distance between Betty and the jet is decreasing at a rate of 750 mph.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






