
2011-2012
Have you ever loved something so deeply, so meaningfully, so completely, so profoundly that it would really irk you if you dropped that thing into a bubbling vat of acid? I have, and so that you may learn from my tragedy, I will share a horrific tale from my past.
Once, on a whim, I spent an entire summer trying to carve a perfect cube from a piece of driftwood on the beach. Don’t ask why; this is what all math teachers do during summer break, and if teachers tell you otherwise, they are lying. Look at their hands carefully—they are probably whittling as they lie to you!
After months of hard work and risking my fish-belly white skin to the sun, I finally found the perfect piece of driftwood. In just a few days, up to my knees in whittled-away wood chips, I beheld the most beautiful hand-carved wooden cube, each edge precisely one inch long. To say it was a thing of beauty is an understatement. In fact, we became fast friends, and spent much time laughing together about the absurdity of life. (I was later to learn that I had a severe case of sun poisoning and may have hallucinated some of this.)
One day I took my little wooden pal to my favorite acid factory. These were the days of the go-go 80s, when you could just walk around giant open vats of hydrochloric acid and take photos, as long as you either wore a hard hat or styled your hair to look like a hard hat. Intent to give my wooden cube the best possible vantage point to see the massive, bubbling vats of acid, I held him precariously over the safety railings.
What happened next? I think you already know. The cube tumbled from my red, blistered fingers into the acid, and the cube vanished from sight. Moments later, it skyrocketed out of the acid, its edges expanding at an absurd 2 ft/sec. I watched with equal parts pride and horror as the cube also gained super crime-fighting powers (including, but not limited to, the power to fly, fill out tax forms correctly, and chew through solid rock). It even retained its perfect cubic shape as it grew to a monstrous size.
I lost consciousness almost instantly, but two moments are seared into my memory, when its still-growing form had an edge length of 12 ft and (later) when the edge length reached an incredible 210 ft.
(a) At what rate did the surface area of the cube change when its edges were 12 feet long? How about 210 feet long?
(b) At what rate did the volume of the cube change when its edges were 12 feet long? Once again, how about later, when its sides measured precisely 210 feet long?
(c) What was the name of the Super Villain whose life ambition was to fight against my beautiful, yet terrifying, cube?
Solution:
(a) First, you need the equation for surface area of a cube, and you’ll take the derivative of it with respect to time. The surface area, s, of a cube is equal to 6e2, where e is the length of an edge. Basically, it’s a collection of six squares, each with an area of e2.
According to the problem, de/dt = 2 ft/sec, and you need to calculate ds/dt. Take the derivative of the surface area formula with respect to time.
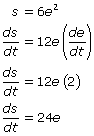
Notice that I plugged in 2 for de/dt. Now you can calculate the two answers required in part (a) by plugging in each, separately, for e:
- When e = 12, ds/st = 24(12) = 288 ft2/sec.
- When e = 210, ds/dt = 5,040 ft2/sec.
Don’t forget units. It’s unnecessary to carry them all the way through, but at least insert them at the end. You use ft2/sec because area is expressed in square units (square feet, in this case, instead of feet).
(b) Apply a technique similar to part (a), using the formula for the volume V of a cube: V = e3.
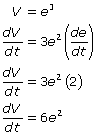
Substitute e = 12 and e = 210 into this formula to get answers of 864 ft3/sec and 264,600 ft3/sec, respectively.
(c) The Super Villian’s name was Butter Fingers, but we will also accept Cameron, the Devourer of Worldsas a correct answer.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






