2011-2012
Let f(x) be the function defined below:
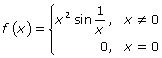
Determine whether f(x) is continuous at x = 0 and explain your answer.
Note: You may use a graphing calculator to examine the graph of f(x).
Solution:
If f(x) if continuous at x = 0, its left- and right-hand limits exist at x = 0, and they are both equal to f(0). Consider the graph of the function below.

This sine curve is a “damped” function; it is already zoomed in quite far, but feel free to zoom in to your heart’s content. The function will wriggle its way to a height of 0 as you approach the y-axis from the right and from the left. Therefore, the general limit exists, and it is equal to 0.
According to the piecewise-defined function, f(0) = 0. (It’s a good thing, too, because substituting 0 intox2sin(1/x) would have been a deal-breaker. You’re not allowed to have a 0 in a denominator.)
Because the limit of f(x) exists as x approaches 0 and it equals f(0), you conclude that f(x) is continuous at 0.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






