2011-2012 Problem 13:
Polar Derivatives
Find all angles on the interval 
at which the tangent line to the graph of the polar equation 
is horizontal.
Solution:
Express the polar equations parametrically (in terms of x and y) and calculate the slope of the polar equation.
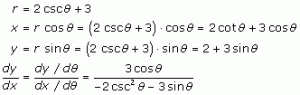
The tangent lines to the polar graph are horizontal when the numerator of this derivative is equal to 0. In other words, at 
.