2011-2012 Chain Rule Problems
Calculate the derivative of tan2(2x –1) with respect tox using the chain rule, and then verify your answer using a second differentiation technique.
Solution for Chain Rule Practice Problems:
Note that tan2(2x –1) = [tan (2x – 1)]2. To find the solution for chain rule problems, complete these steps:
- Apply the power rule, changing the exponent of 2 into the coefficient of tan (2x – 1), and then subtracting 1 from the square.
- Multiply by the expression tan (2x – 1), which was originally raised to the second power.
- Take the derivative of tan (2x – 1) with respect to x.
- Multiply by the derivative of 2x – 1, the expression that is plugged into tangent.
Derivative of tan2x
These four steps are implemented in the solution below for derivative of tan2x.
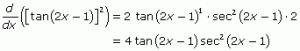
To verify the derivative, apply the product rule, noting that tan2(2x –1) = tan (2x –1) · tan (2x – 1). Evev the product rule will require the chain rule, when you differentiate each factor (2x – 1), as demonstrated below.
Both techniques for these chain rule practice problems result in the same derivative.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.
