
2019-2020
Find the antiderivatives of each with respect to x, without using u-substitution (i.e., without changing variables):
(a) 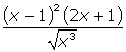
(b) ![]() , assuming a, b, c, d, and e are constants
, assuming a, b, c, d, and e are constants
Integral Power Rule Solution:
(a) For the integral power rule solution, start by expanding the numerator, squaring (x – 1) and mutliplying by (2x + 1). Rewrite the denominator as a term with a negative exponent, and then distribute it through the quantity.
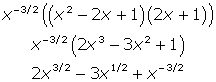
Now you can antidifferentiate by adding 1 to each power individually and multiplying the coefficient by the reciprocal of the resulting exponent. In other words, for the first term, add 1 to 3/2 to get 5/2. Then, multiply 2 by the reciprocal of 5/2, which is 2/5.
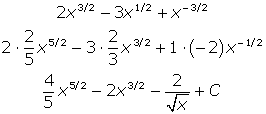
Don’t forget that a general antiderivative (i.e., an indefinite integral) must always contain “+ C.”
(b) Follow the same procedure, beginning by writing the radical term with a fractional exponent. Then, distribute and find the antiderivtaive. The variables make it marginally more difficult, especially when you add 1 to the weird variable powers.
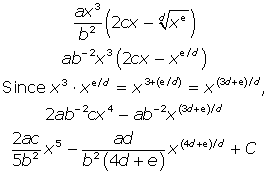
Integrals of radical functions
To apply the power rule for integration to this type of function, you have to remember an important rule from algebra.
If we can write the function using exponents then we most likely can apply the power rule.
Let’s solve this problem:
∫ √x+4 dx
Before even using any calculus, you can rewrite the function using the above rule with exponents. So, you have exponents and can apply the power rule.
It becomes:
∫√x + 4 dx = ∫x^1/2 +4 dx
Then, you can apply the power rule.
It then becomes:
∫ x^1/2 +4 dx= (x^(1/2+1)) / ( 1/2 + 1) + 4x + C
When simplified, you get the final answer.
That is:
(x^3/2 / 3/2) + 4x + C
Which equals:
(2/3 * x^2/3) + 4x + C
The final answer can usually be written with exponents, like we did here. Or, it can be written with roots. However, your teacher or professor may have a preference, so make sure you ask!
Finding the Power Rule for Integration
As with anything else related to calculus, perfecting the power rule for integration will take a lot of practice if it doesn’t come to naturally.
Make sure you look up practice problems online! You can browse our other calculus problems here. Best of luck!
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






