Sometimes, one of the hardest things about calculus is remembering how to apply the different rules. For that reason, anything that helps you remember how to work out equations and makes calculus easier is worth learning, right?
The calculus quotient rule is a great example of a concept in calculus that can be easily memorized to help you perform calculus quicker and more efficiently.
So let’s take a look at how to do it.
What is the quotient rule?
To put it simply, the quotient rule is a method for differentiating problems where one function is divided by another. The quotient rule allows you to find the derivative of a quotient of two functions – hence the name.
The theory behind the calculus quotient rule goes like this:
Anytime you have two differentiable functions – let’s use f(x) and g(x) as an example – the quotient must also be differentiable.
If it makes it easier, you can think of it like this: the derivative of the quotient of these two functions must exist.
And there’s a formula to express this basic fact:
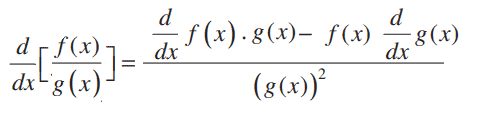
This formula can help you find the derivative of a function that is written in the form of a quotient, so any fraction where the numerator and the denominator are both functions of the variable x.
Looking at that formula, it might seem unlikely that you can commit that to memory. But actually, there is a way to remember this formula so you always have it at the tip of your fingers when you need it.
Using the Quotient Rule
The trick to using the calculus quotient rule is to always start with the bottom function, and to end with the bottom function squared. Some people remember this with the phrase “Hi Dee Ho”!
The top function is ‘Hi’ in this scheme. That makes the bottom function ‘Ho,’ since it’s low.
So a way to remember this formula is with the phrase, “Ho Dee Hi minus Hi Dee Ho over Ho Ho.”
The ‘dee’ in the phrase stands for the derivative.
In words, it means: “The derivative of the quotient of two functions is equal to the bottom function times the derivative of the top function, minus the top function times the derivative of the bottom function, all divided by the bottom function squared.”
Still confused? Let’s take a look at some examples to make things clearer.
Example 1
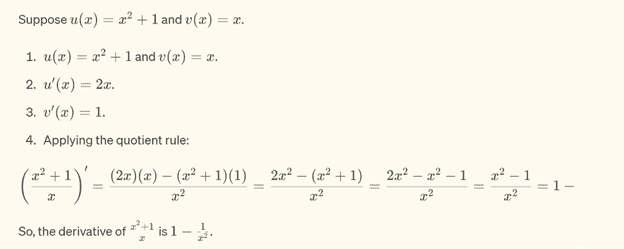
Example 2
Next, let’s look at an equation that demonstrates the common mistake people make when using the calculus quotient rule.
It’s important to remember that the derivative of a quotient is not equal to the quotient of the derivatives. That’s a mistake people often make because it seems like it should be, but it’s important not to fall into this trap when using the quotient rule.
Hopefully, this equation will make it clear what I mean:
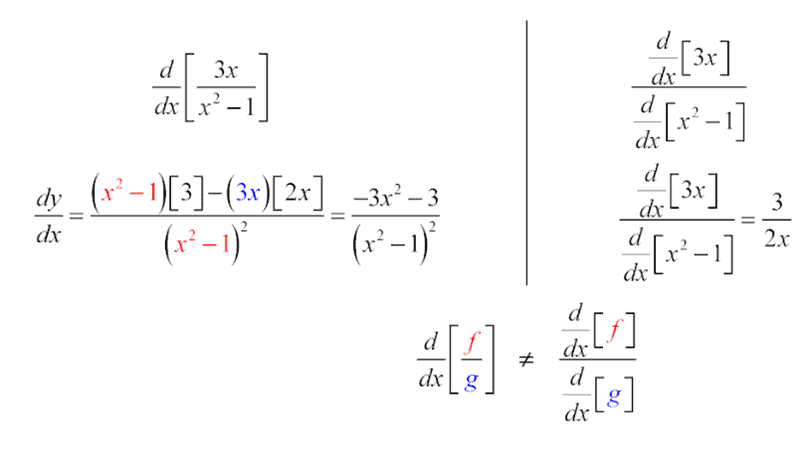
Example 3
Now let’s look at how the quotient rule can help you figure out the instantaneous rate of change at a given point:

Uses of the Quotient Rule
So often, calculus can seem abstracted from the real world. But as we all know, mathematics is the secret language the universe speaks, and calculus is no exception. The quotient rule does indeed have some very useful applications in the real world for those who know how to use it correctly.
Here are some potential uses of the quotient rule:
- Physics:
- Velocity and Acceleration: In kinematics, the quotient rule can be used to find the rate of change of velocity with respect to time when velocity is given as a quotient of two functions.
- Optics: The rule can be used in studying light refraction and the behavior of lenses where functions might be divided.
- Economics:
- Marginal Cost and Revenue: When cost or revenue functions are expressed as ratios, the quotient rule helps in determining the marginal values.
- Elasticity of Demand: Elasticity is often expressed as a ratio of percentage changes in quantity and price, and its derivative can be found using the quotient rule.
- Biology:
- Population Dynamics: In models where population growth rate is expressed as a ratio of two functions (e.g., predator-prey models), the quotient rule can be used to analyze changes over time.
- Enzyme Kinetics: In biochemical reactions, the rate of reaction might be given as a ratio of concentrations, and the quotient rule helps in studying these rates.
- Engineering:
- Control Systems: Transfer functions in control systems are often expressed as quotients of polynomials. The quotient rule is used to analyze system stability and response.
- Signal Processing: In analyzing signals and systems, the quotient rule helps in differentiating transfer functions and other related expressions.
- Mathematics:
- Differential Equations: In solving differential equations where solutions might be in the form of a ratio of functions, the quotient rule aids in finding derivatives.
- Optimization Problems: When dealing with optimization of ratios, such as maximizing efficiency or minimizing cost per unit, the quotient rule helps in finding critical points.
- Chemistry:
- Reaction Rates: In chemical kinetics, reaction rates are often expressed as ratios, and the quotient rule can be used to differentiate these expressions.
- Equilibrium Constants: In thermodynamics, equilibrium constants are expressed as ratios, and their derivatives with respect to temperature or pressure can be analyzed using the quotient rule.
Mastering the Quotient Rule
Hopefully, this article has helped demystify the quotient rule. Once you’ve mastered the ‘Hi-Dee-Ho’ mnemonic device, you may find that this rule comes to you quicker than you might have expected from looking at the formula alone.
And whatever you need to master this rule for, you’ll find it’s a useful way to find derivatives in calculus.