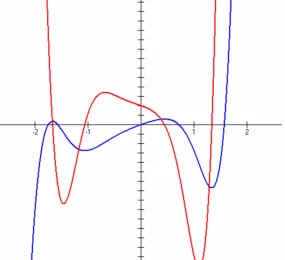
The derivative of arccos in trigonometry is an inverse function, and you can use numbers or symbols to find out the answer to a problem. It uses a simple formula that applies cos to each side of the equation. Some people find using a drawing of a triangle helps them figure out the solutions easier than using equations.
The derivative of Arccos is used in trigonometry. It’s an inverse function, and you can manipulate it with numbers or symbols. There are several terms you’ll need to know when working with Arccos, including radian.
Arccos means arccosine. You may also work with arcsin, or arcsine when working with trigonometry problems.
Results for the derivative of Arccos are written in radians. Solving a problem involving Arccos first requires knowledge of radians.
An Overview Of Radians
Image by Pixabay
Radians are used to measure angles. The angle of a single radian subtends or creates an angle. At a certain point, extremities present straight lines that join at that particular point. When two rays pass through the arc endpoints, the angle is subtended.
The radian has an angle of a single radian subtended from a unit circle’s center. A radian creates an arc length of 1. Therefore, we can determine that a full angle measures 2pi radians. The angle contains 360 degrees for every 2pi radians, which is equivalent to 57.29577951 degrees per radian or 180 degrees pi.
A right angle measures pi/2 radians. A straight angle measures pi radians. Radians let you write integrals and derivative easily, like d/(dx)six equals cosx when x is measured by radians.
The Difference Between Geometry And Trigonometry

Image by Pixabay
The three branches of mathematics are algebra, arithmetic, and geometry. Geometry is the study of sizes, properties, and shapes of spaces of three- dimensional and two-dimensional objects. Euclid, the Father of Geometry, is often mentioned in conjunction with theorems and postulates about the field.
Geometry is a combination of the Greek terms Geo (earth) and metron (measure). You will encounter solid, spherical and plane geometry in your studies.
Spherical geometry is the study of three-dimensional objects such as spherical polygons and spherical triangles. Plane geometry features lessons about two-dimensional objects such as points, curves, lines, and planes, including polygons, circles, and triangles. Solid geometry focuses on spheres, prisms, cubes, pyramids, and other three dimensional objects.
Euclidean Geometry is the study of flat surfaces, and it’s just one of the branches of geometry. Riemannian geometry, the study of curved surfaces, is another major branch of geometry.
Trigonometry is a branch of geometry. The field emerged in about 150 B.C. when a mathematician named Hipparchus used sine to make a trig table.
Trigonometry deals with triangles, their lengths, and their angles. You can also use trigonometry to study waves and oscillations. You will study the way the side lengths of right triangles relate to each other. The basic relationships between triangles and their sides are referred to as Sine, Tangent and Cosine.
If you have a right angle triangle, the longest base is referred to as the hypotenuse. The side in front of an angle is its opposite side, and the adjacent side is the side behind that angle. The relationship for a right angle triangle then is sin A, or the opposite of the hypotenuse, cos A, the adjacent side of the hypotenuse, and tan A the opposite/adjacent side.
The secondary relationships in trigonometry are:
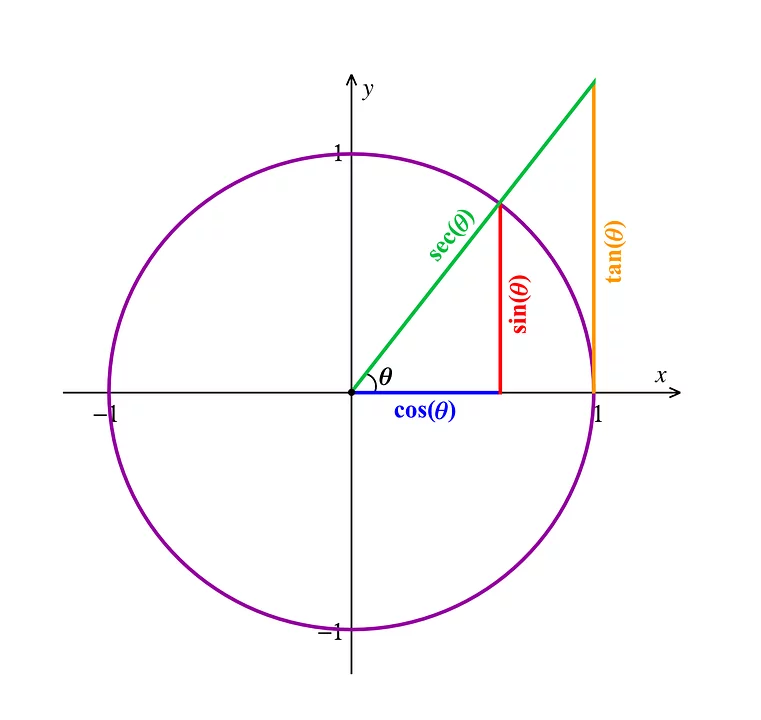
Image by Pixabay
These measurements are the respective dimensions of Sine, Cosine, and Tangent.
Spherical trigonometry that deals with triangles in 3D scenarios, and it’s used in navigation and astronomy.
Trigonometry helped ancient sailors navigate the seas. Today, trigonometry has many uses beyond math class.
Oceanographers use trigonometry to figure out the height of ocean tides or measure sea animals. Trigonometry can be used to build ships and help them navigate. This mathematical field also helps criminologists determine the trajectory of bullets and other projectiles.
Archeologists divide their excavation sites up for work using trigonometry. Flight engineers use trigonometry to determine the best flight course for a plane. Trigonometry helps fill in the “third side” of a flight’s wind, speed, and direction equation to make sure the plane goes in the right direction.
Example 1

Image by Pixabay
In trigonometry, the Arccos means cos to the negative first power (z) or the arc cosine of the complex number represented by (z). You will consider that this problem involves an inverse trigonometry function and write down two identities:
Cos (cos to the negative 1st power(x)) equals x, then cos to the negative 1st (power (cos(x)) equals x.
You need to decide which formula to use. You should use the first formula, due to the chain rule. The chain rule allows you to find the derivative for the term cos−1
(x) more easily than using the first formula. Simply the formula to cos (y) equals x. Now you have an implicit formula to solve the problem and determine y.
Use implicit differentiation to find out the answer for y’.
(cos(y))0 = (x)followed by y’ (− sin(y)) = 1 and y’ equals negative 1 over sin (y), then y’ equals negative 1 over sin(cos to the negative 1st power(x)).
The formula written above is an excellent tool, but there is an even better way to write it using geometry instead of algebra. Cos has an angle and a number between negative 1 and 1, cos negative one will also give angle and have a number between negative 1 and 1.
Now define θ equals cos minus 1(x)to show the angle cos negative 1. Therefore, x equals cos (θ), according to the inverse function. You can also use cos with both sides of the function.
Drawing a triangle can also help you find the answer to this problem. Draw a triangle with points ABC and θ will be the angle less than C. Cos (θ) equals ACBC in geometry, and cos (θ) also equals x.
Consider that BC equals 1 and AC equals x. You could choose any identity in the above values, but the most obvious ones make the math easier.
In the triangle example, sin(θ) = AB over BC. Use the Pythagorean Theorem to calculate the answer for sin(cos−1(x)), which is equal to sin(θ).
Here’s the solution per the Pythagorean Theorem:
BC squared equals AB squared plus AC squared, followed by AB squared equals BC squared minus AC squared. Therefore, AB squared equals one minus x squared, and AB equals the square root of 1 minus x squared.
The equation calculated above answers the question correctly. Sin(cos negative 1 (x)) equals sin(θ) equals AB over BC equals AB equals the square root of 1 minus x squared. Complete the answer with
Example #2
Image by Pixabay
This problem demonstrates how to determine the derivative of Arccos x and Arcsin x.
The equation you use is d over dx (arcsin x plus arccos x) equals zero. Note that arcsin x plus arccos x equals pi over 2. You can explain this equation with the following calculations:
If arcsin x equals zero, then x equals sinθ equals cos( pi over 2 minus θ), then arccos x equals pi over 2 minus θ equals pi over 2 minus arcsin x; therefore arcsin x plus arccos x equals pi over 2.
Example #3

Image by Pixabay
The derivative you find for arccos x will be the negative of arcsin x’s derivative. This derivative stature holds for the inverse of each cofunction pair.
The same formulas apply to similar trigonometry problems. Arccot x’s derivative is the negative of arctan x’s derivative. Arcsec’s derivative is the negative of the derivative of arcsecs x.
The variable y equals arcsec x, represent tan y equals plus-minus the square root of x to the second power minus one.
Begin solving the problem by using y equals arcsec x, which shows sec y equals x. Now use Pythagorean identity b to figure the next step.
Tan y equals plus minus the square root of sec squared y minus 1 equals plus minus the square root of x squared minus 1. Y’s derivative equals arcsin x.
The equation then is d over dx arcsin x equals one over the square root of one minus x squared. Prove this by looking at y equals arcsin x, which stands for sin y equals x. Figure the derivative of x with the following equation:
Cos y followed by dy over dx equal 1, then dy over dx equals 1 over cos y’, then dy over dx equals 1 over the square root of 1 minus x squared ‘.
An alternate theorem for this would be d arcsin x over dx equals 1 over din sin y over dy equals 1 over cos y equals 1 over the square root of 1 minus x squared.
Arccos X Functions
The arccosine of x is the representation of the inverse cosine function of the variable x when negative 1 is less than x and x is less than 1. If the cosine of y equals x, the arccosine of the variable x is equal to x’s inverse cosine function, which equals y. The equation for this function reads arccos x equals cos to the inverse cosine x equals y.

Image Source: Pixabay
The equation is written arccos 1 equals cos, followed by the negative 1 symbol, which stands for inverse cosine function in this problem.
Therefore, arccos 1 equals cos negative 1 (inverse function), and 1 equals zero, and Rad equals zero degrees.
–>